热力学名词

流体/固体界面

温度场和热通量在流体/固体界面连续，然而在运动的流体中，温度场会快速变化：在靠近固体处，流体的温度与固体接近；但在远离界面的地方，流体温度则接近于入口或周围流体的温度。流体温度从固体温度变为流体整体温度的区域称作热边界层。利用 Prandtl 数(\(P_r=C_p/\mu k\)) 来表示热边界层的大小与动量边界层的相对大小：当 Prandtl 数等于 1 时，热和动量边界层的厚度应相同；当Prandtl 数大于 1 时，动量层较厚；与之相对，当 Prandtl 数小于 1 时， 动量边界层要薄于热边界层。20°C 大气压下，空气的 Prandtl 数为 0.7；这是由于空气中动量和热边界层的尺寸类似，但动量边界层略薄于热边界层。20°C 水的 Prandtl 数为 7；因此，水温在靠近壁面处的变化要比速度变化更剧烈。

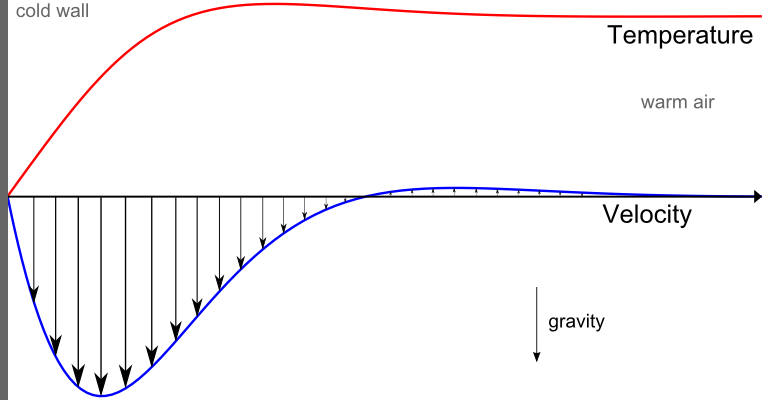靠近较冷固体壁面处的自然对流空气的归一化温度(红色) 和速度 (蓝色) 曲线

自然对流

自然对流模式对应由浮力效应驱动流动的结构。基于预期的热性能，自然对流可能有益（例如在冷却应用中），也可能有害（如绝热层中的自然对流）。

Rayleigh 数 \(Ra\)用于表征由自然对流带来的流型和传热。Rayleigh 数由流体材料属性、空腔尺寸 \(L\) ，以及温差 \(\Delta T\) 定义，而温度差则根据流体周围的固体来设定： $$ Ra=\frac{\rho^2g\alpha_p C_p}{\mu k}\Delta T L^3 $$

Grashof 数是另一个流型指标，它是浮力相对粘性力的比例： $$ Gr=\frac{\rho^2g\alpha_p}{\mu^2}\Delta T L^3 $$

Rayleigh 数可通过 Prandtl 和 Grashof 数的关系式表示： $$ Ra=Pr Gr $$ 如果 Rayleigh 数较小（通常\(<10^3\)），则可以忽略对流，大部分传热由流体中的传导造成。

于较大的 Rayleigh 数，则需要考虑对流传热。浮力相对于粘粘力较大时，流型为湍流，否则为层流。两个流型之间的过渡由 Grashof 数的临界阶次确定，即 \(10^9\)。当 \(Pr\) 的量级近似为 1 或更大时，热边界层，即固体壁面和流体整体之间的典型温度转变距离，可近似为 $$ \delta_\mathrm{T} \approx \frac{L}{\sqrt[4]{Ra}} $$

当与热表面接触时，一杯冷水中的自然对流所带来的温度剖面图

强制对流

强制对流模式对应于这一结构：流动由带来主要浮力效应的外部现象（例如、风）或器件（例如、风扇和泵）驱动。

此时，流型可使用雷诺数作为指标近似表征为等温流： $$ Re=\frac{\rho U L}{\mu} $$ 雷诺数代表了惯性力对粘性力的比例。当雷诺数较低时，以粘性力为主，并能观察到层流；当雷诺数较高时，系统阻尼非常低，会带来较小的扰动；如果雷诺数足够高，流场最终将演变为湍流的流型。

可以使用雷诺数计算动量边界层的厚度，即 $$ \delta_\mathrm{M} \approx \frac{L}{\sqrt{Re}} $$

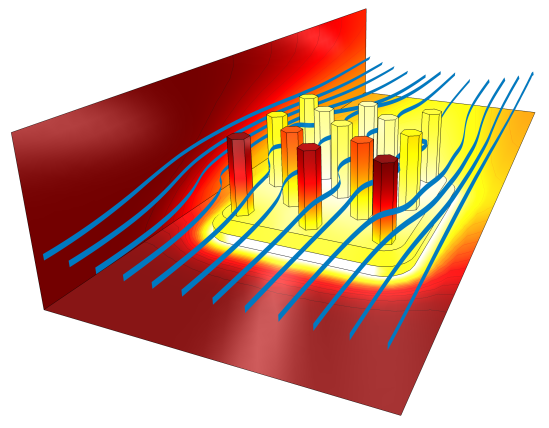由强制对流提供冷却的散热器周围的流线和温度剖面图

辐射传热

辐射传热可以与上文介绍的对流和传导传热相结合。

在大部分应用中，流体相对热辐射是透明的，固体则为非透明。因此，辐射传热可表示为表面对表面辐射，在实体壁面之间通过透明的空腔传递能量。由漫反射灰体表面所发射的辐射热通量等于 \(\varepsilon n^2 \sigma T^4\)。当一个表面被带有均匀 \(T_\mathrm{amb}\) 的物体包围时，净辐射通量为 $$ q_\mathrm{r}=\varepsilon n^2 \sigma (T_\mathrm{amb}^4-T^4) $$ 当围绕表面的温度不同时，每个表面对表面的交换则由表面的视角因子确定。

不过，流体和固体都可以是透明或半透明的；因此辐射可以在流体和固体中发生。在参与（或半透明）介质中，辐射线将与介质（固体或流体）相互作用，随即吸收、释放和散射辐射。

温度差较小且发射率较低的应用中，可以忽略辐射传热；但在温度差较大且发射率较高的应用中，辐射传热相当重要。

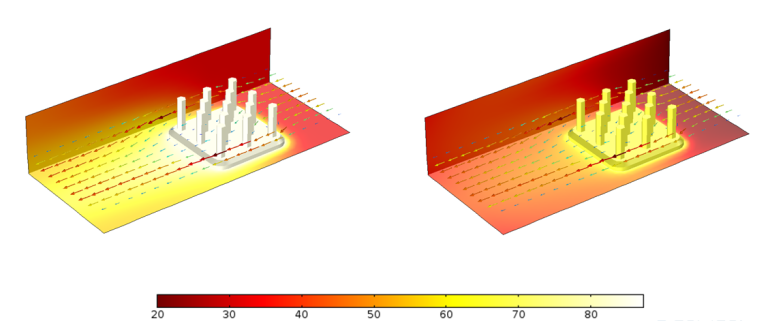表面发射率分别为 \(\varepsilon=0\) （左）和 \(\varepsilon=0.9\) （右)的散热器温度剖面图对比