基于新型蜘蛛网状通道冷却板交换器的锂离子电池热管理数值研究

原文标题：Numerical research on lithium-ion battery thermal management utilizing a novel cobweb-like channel cooling plate exchanger

作者：Qian Zhao 1,2 Huawei Wu 1,2 Zhaohui Wang 3 Yiwei Fan 3 Wei Cheng 4

1. Hubei Key Laboratory of Power System Design and Test for Electrical Vehicle, Hubei University of Arts and Science, Xiangyang, China
2. School of Automotive and Traffic Engineering, Hubei University of Arts and Science, Xiangyang, China
3. Key Laboratory of Metallurgical Equipment and Control Technology of Ministry of Education, Wuhan University of Science and Technology, Wuhan, China
4. Xiangyang Public Inspection and Testing Center, Xiangyang, China

1 简介

近年来，随着世界各国能源危机和环境污染问题日益突出，纯电动汽车得到了快速发展。动力电池模组作为电动汽车三大核心技术之一，对于整车的稳定性和安全性至关重要（Lu et al., 2020）。锂离子电池作为汽车电池模块中使用最多的电池，具有使用寿命长、能量密度高、自放电率低等诸多优点( Yang W. et al., 2020）。然而，锂离子电池也有很多缺点，比如对温度的要求较高，研究表明，锂离子电池最合适的工作温度范围是 20~40℃，温差在 5℃ 以内（Pradeep 和 Venugopal，2020；Yang Y 等人，2020）。温差过大以及温度过高或过低都会对电池性能产生较大影响，造成电池容量、性能下降和使用寿命缩短等不良变化，严重时会造成电池热失控（Al-Zareer 等人，2019）。为了防止此类现象的发生，为电池设计有效的热管理系统显得尤为重要。

目前，根据冷却介质的不同，动力电池模组的冷却方式主要分为三种（Kausthubharam 等，2021）：风冷（Yu 等，2019；Xie 等，2019）、液体冷却（Qian et al., 2016；Patil et al., 2020）和相变材料冷却（Wilke et al., 2017；Huang et al., 2018；Choudhari et al., 2020））。风冷根据系统是否添加强制通风技术分为自然对流冷却和强制通风冷却，但随着对电池安全性、充电速度等性能要求的不断提高，风冷已不再能够高效散热来自电池（Saw 等人，2016；Zhao 等人，2016）。利用相变材料实现电池散热的冷却方法需要安装另一套冷却系统来辅助散热，较高的维护成本也限制了其在电池热管理系统中的应用( Alipanah and Li，2016 ；Li et al .等，2018）。因此，散热效率更高、成本更低的液冷方式对于电池模组散热优势更加明显，能够有效防止锂离子电池在高倍率放电下的过热现象（Imran et al., 2018 ）。

在液冷冷却方法中，基于微通道冷却板的冷却系统通常用于控制电池温度。张等人。(2017)采用基于冷却板的方法成功地将动力电池温差控制在最佳范围内。贝希等人。(2020)通过实验证明，微通道冷却板可以在 8°C 放电倍率条件下有效散发电池热量，从而防止电池热失控。盛等人。(2019)开发了具有双入口和出口的蛇形通道冷却板。利用 FloEFD 软件分析了不同工况下冷却液流向、流量、通道宽度对电池温度分布的影响，结果表明冷却液流向和冷却板通道宽度对电池温度分布影响较大。电池温度分布与冷却板的功耗比有关，增加流体流量显着降低了电池模块的最大温升，但对温度分布影响不大。拉奥等人。2016，饶等人。2017 年设计了圆柱形电池模组的平行通道冷却板，分析了通道数和冷却接触面积对电池冷却性能的影响，得出增加冷却板通道数和电池间接触面积的结论。冷却板可以有效降低电池的温升，对电池温度均匀性的提高也有显着的作用。钟和金，2019 参考典型的翅片冷却结构，建立了基于液冷的软包电池组的热模型。从冷却性能和温度均匀性方面检查电池组的热行为。数值结果表明，翅片排列的不对称设计对电池组的温度均匀性产生负面影响。霍等人。(2015)设计了一种基于平行通道板的电池热管理系统，用于冷却矩形锂离子电池，并研究了通道数、流向、入口质量流量和环境温度对电池放电过程温升和温度分布的影响。结果表明，电池的最高温度随着通道数和入口质量流量的增加而降低。并且冷却性能随着质量流量的增加而提高，但增加的趋势变小。

经典的蛇形流道和平行流道具有良好的散热性能，但由于其结构对冷却液的流动方向有一定的限制，难以进一步提高冷却板与电池模组之间的热交换性能。启发借鉴生物学中的蜘蛛网结构，设计了一种入口和出口不对称的蛛网型（C 型）通道冷却板。以蛇形通道冷却板为对比，数值研究了冷却剂流向、冷却通道尺寸和间距以及冷却板厚度对电池温度分布和通道压降的影响，分别。在此基础上，利用正交试验方法得到了蛛网状通道的最优参数组合，为电池热管理系统的设计提供了思路。

2 模型与方法

2.1 物理模型

图 1A 显示了锂离子电池液体冷却装置的简化几何模型。电池模组底部填充热界面材料（TIM）以紧密贴合冷却板，电池模组产生的热量通过 TIM 传导至冷却板。表面，然后热量被冷却剂带走。图 1B 为蜘蛛网状通道冷却板的结构示意图。冷却通道由内向外呈放射状，其形状类似于蜘蛛网。通道横截面为圆形，通道 1-4 通过 U 型通道连接。各通道间距相等，具体结构参数见表 1。此外，冷却通道的显着特点是入口和出口（a 和 b）不对称，这使得冷却液形成两个不同的流动方向。第一流向（以下简称“ Ifd ”）是冷却液从 a 口流入，从直管流入通道 1，经过 U 型通道，进入通道 2、通道 3 和通道 4 分别从 b 口流出。第二流向（以下简称“ II fd ”）为冷却液从 b 口流入通道 4，分别经过通道 3、通道 2、通道 1，最后从端口 a 流出。

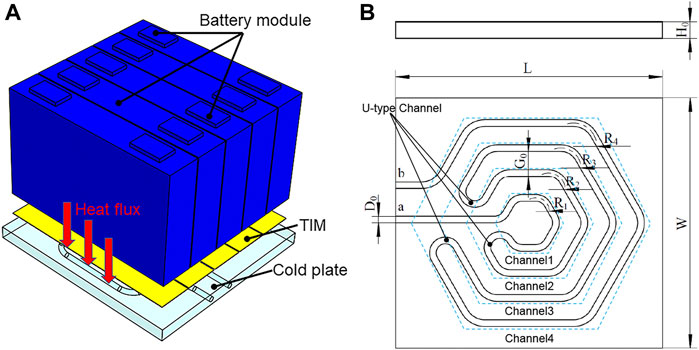
图 1 (A) 基于蛛网状通道原理图的电池冷却结构示意图 (B) 冷却板结构示意图

表 1. 冷却板结构参数

2.2 电池发热模型

锂离子电池的内部由堆叠的电芯组成。在放热过程中，涉及反应热、焦耳热等各种热。计算这些热量时需要考虑复杂的化学反应、发热和材料的导热性。因此，需要建立合理的电池发热率模型。本文采用广泛使用的 Bernardi 电池发热率数学模型，其发热率方程由下式描述：（伯纳迪等人，1985）。在不考虑电池滥用或热失控状态（极限状态）的工况下，基于 Bernardi 电池生热和热传导理论，结合电池内部材料的分布规律，适当设计电池芯的结构简化。假设电池内部是均质材料，无论温度和充电状态如何，电池的密度、比热容和热导率都保持恒定。忽略电池内部的对流传热和热辐射，就是关注整个电池模组与冷却板之间的传热。目的是平衡模型精度和复杂度之间的关系

\[ q=\frac1{V_b}\left[I^2R+T\left(\mathrm{d}E_0/\mathrm{d}T\right)I\right] \]

其中\(q\)为锂离子电池单位体积的发热功率，\(V_b\)为电池发热部分的体积，\(I\)为充放电电流，\(I^2 R\)为电池产生的焦耳热，\(R\)为电池内阻，\(T\left(\mathrm{d}E_0/\mathrm{d}T\right)I\)代表电池产生的可逆反应热，\(T\left(\mathrm{d}E_0/\mathrm{d}T\right)\)为温度系数，\(E_0\)为开路电压，\(T\)是电池温度。

本工作中，所选方形锂离子电池的技术规格和热物理参数如表 2所示。

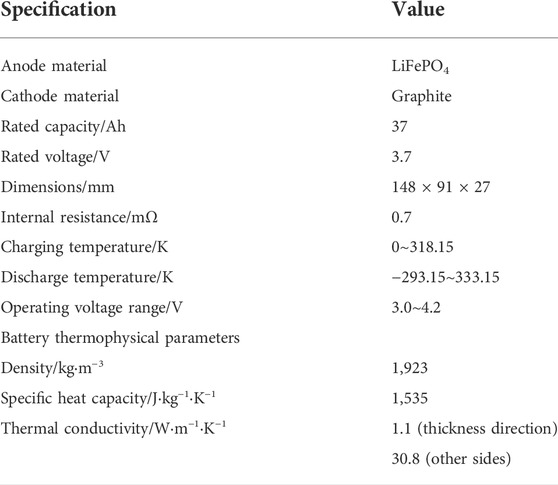
表 2 . 锂离子电池参数。

2.3 数值解

2.3.1 计算流体动力学理论

为了简化模拟，假设如下：

(1)冷却板是均匀各向同性的。

(2) 冷却板除上表面外的表面均假定为绝热。

(3)流体是不可压缩的稳定流体，具有恒定的动力粘度、比热容和导热系数，无内部热源。

(4)流体和固体的热物理性质与温度无关。

(5) 忽略重力、粘性耗散和热辐射的影响。

此外，雷诺数是判断流体运动状态的重要参数。冷却通道入口处的雷诺数可按下式计算：冷却剂的雷诺数小于临界雷诺数 2,300。因此，本工作涉及的流体运动模型为层流模型。

\[ R_e=\frac{\rho_cD_hv_c}\mu \]

其中\(R_e\)为雷诺数，\(\rho_c\)为流体密度，\(D_h\)为特征长度，\(v_c\)为流体速度，\(μ\)为流体粘度系数。

基于上述假设，稳态工况下无内热源的不可压缩层流控制方程简化如下：

连续性方程：

\[ \frac{\partial u_j}{\partial x_j}=0 \]

动量守恒方程：

\[ \frac{\partial(\rho u_j)}{\partial t}+\frac{\partial(\rho u_ju_i)}{\partial x_j}=-\frac{\partial p}{\partial x_i}+\frac\partial{\partial x_j}\left(\frac{\mu\partial u_j}{\partial x_j}\right) \]

能量守恒定律：

\[ \frac{\partial(\rho T)}{\partial t}+\frac{\partial(\rho Tu_j)}{\partial x_j}=\frac\partial{\partial x_j}\left(\frac\lambda{c_p}\frac{\partial T}{\partial x_j}\right) \]

固体能量守恒方程

\[ \nabla^2T=0 \]

其中，\(u\)、\(x\)、∇ 分别为直角坐标系中的速度矢量、矢量算子和梯度算子，\(\rho\)为流体密度，\(p\)为流体压力，\(\mu\)为流体动力粘度，\(cp\)为流体比热容，\(\lambda\)是流体的热导率，\(T\)是温度。

通道圆表面与流体之间的热量传递\(q\)可用牛顿冷却公式计算

\[ q=hA\left(T_w-T_l\right) \]

式中\(h\)为对流换热系数，\(A\)为对流换热面积，\(T_w\)为流道圆表面温度，\(T_l\)为冷却剂温度。

为了简单起见，电池模块的最高温度（\(T_ {max}\)）和温差（\(\Delta T\)）将表明电池工作状况的好坏。最高温度和温差越大，表明电池模组的工作状况越差，散热板的性能也越差。另外，当通道内流体为不可压缩层流时，冷却板通道入口与出口之间的压降（\(\Delta p\)）如下

\[ \Delta P=\frac{v^2fl\rho}{2D}=P_{inlet}-P_{outlet} \]

式中，\(v\)为流体速度，\(l\)为通道沿流动方向的长度，\(\rho\)为流体密度，\(D\)为通道水力直径，\(f\)为摩擦系数。\(P_{inlet}\)和 \(P_{outlet}\)分别是入口和出口的总压力。

2.3.2 网格独立性测试

在计算流体力学（CFD）数值模拟中，模型中网格的质量和数量对模拟的精度有重要影响，因此获得良好的网格是模拟计算的前提。本工作采用 STAR-CCM+软件的网格模块进行网格划分。电池模块、冷却板和冷却剂采用收敛性好、计算精度高、内存消耗低的多面体网格，厚度较小的热界面材料采用两层薄体网格。此外，为了获得更准确的传热模拟结果，对冷却剂的流体部分进行了加密，在流体与冷却板通道的交汇处建立了 5 个边界层，

为了确定合适的网格数量，利用图 1B中的冷却板结构进行网格独立性验证。首先利用 STAR-CCM+生成 6 种不同数量和网格质量在 0.95 以上的体网格，然后在相同边界条件下对网格数量对最高温度（\(T_ {max}\)）的影响进行数值模拟电池模块的温度差（\(\Delta T\)）、冷却板进出口压降（\(\Delta p\)）并网独立性测试结果如图 2A 所示。结果表明，当网格数达到 1160828 并进一步增加网格数时， \(T_ {max}\)、\(\Delta T\)、\(\Delta p\)的变化均小于 1%。这表明模拟结果与体积网格数无关。因此，综合考虑实际计算条件，最终确定网格基本尺寸为 0.01 m，网格总数为 1160828，网格质量为 0.98（最佳网格质量为 1）。网格模型如图 2B、C所示。

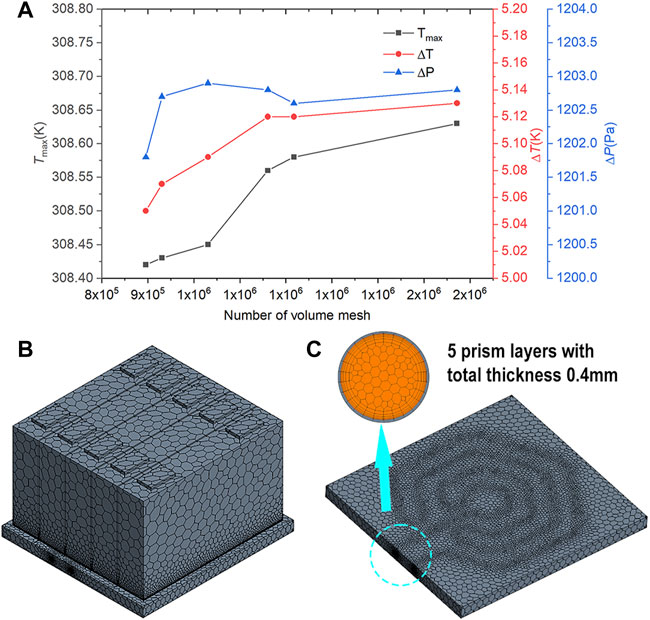
图 2 (A)网格独立性测试 (B)电池模块的网格模型 (C)冷板

2.3.3 边界条件

在本文中，入口边界定义为速度入口，设置为 \(0.3 m/s\)，温度设置为 \(299.15 K\)，出口边界定义为压力出口，设置为 \(0 Pa\)。冷却板材料为铝，冷却液材料为水，电池模组与冷却板之间填充热界面材料，以提高冷却板与电池模组之间的热交换性能。电池的热源设置为体积热源。具体参数值如表 3所示。

表 3. 冷却系统参数设定

3 结果与讨论

3.1 分析比较

在 3C 放电条件下，设置相同的边界条件，分别模拟两个冷却剂流动方向（ Ifd和IIfd）上的蛇形（S 型）和蜘蛛网状（C 型）通道。由此获得电池模块、冷却板和冷却液的温度场以及冷却通道的压力分布。

图 3A-C显示了电池模块温度分布的比较。如图 3A所示，电池模组表面温度沿冷却液流动方向逐渐升高，且存在明显的温度梯度。最低温度在冷却液入口处，其值为 302.95 K，最高温度为 309.18 K，温差为 6.23 K。因此，S 型冷却板对电池模块的散热效果并不理想。图 3B、C显示了采用 C 型冷却板的电池模块的温度分布。如图 3B所示，使用I时流向电池模块的冷却液的最高温度Ifd下降至 \(308.81 K\)，温差为 \(5.66 K\)，温度分布得到一定改善。同时，如图3C 所示，IIfd的电池表面温度分布更加均匀，电池的冷却效果最好，最高温度为 \(308.56 K\)，温差也降至$ 5.12 K$。

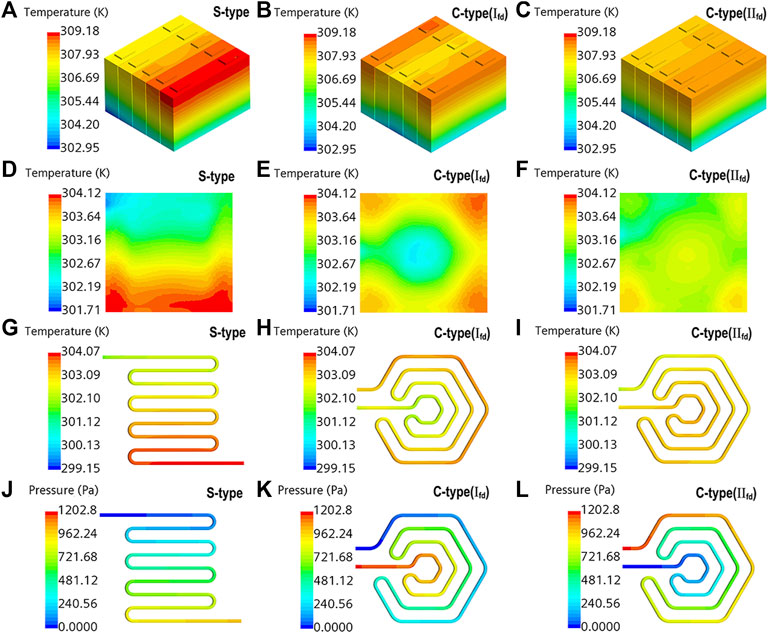
图 3. (A-C)电池模组表面温度分布；(D–F)冷板；(G–I)冷却剂；(J–L)冷却通道的表面压力分布。

冷却板表面的温度分布可以间接反映两种结构的冷却性能( Deng et al., 2019; Yan et al., 2019 ; Fan et al., 2022 )。图 3D-F显示了冷却板表面温度分布的比较。如图 3D所示，S 型冷却板表面温度分布变化较大，最高温度为 \(304.12 K\)，最低温度为 \(301.71 K\)，温差为 \(2.41 K\)。高温主要集中通道出口附近，与电池模组的温度分布一致。如图 3E、F所示，冷却板表面温度分布比 S 型冷却板更均匀。使用 Ifd的 C 型散热板表面较高温度主要集中在角落，最高温度为 \(304.01 K\)，较低温度分布在散热板中部，最低温度为 \(302.09 K\) ，温差为 \(1.92 K\)。而IIfd的最高温度下降到 \(303.66 K\)，温差下降到 \(1.5 K\)。因此，发现流向IIfd使得冷却板的温度控制在较小的范围内，温度分布更加均匀，更有利于冷却板发挥最佳的热交换性能，从而保证电池模组的有效散热。

图 3G-I显示了冷却液的温度比较。对于 C 型来说，采用 IIfd的冷却液最高温度和温差更小，温度分布更均匀，有利于减小电池表面的温差，使电池能够更好地发挥作用表现。S 型冷却液的温度分布呈两极分化，出口温度远大于入口温度，导致温差过大，会对电池的正常工作产生较大影响。此外，如图3J-L 所示，使用I fd冷却通道入口和出口之间的压降 IIfd 和IIfd分别为 \(1,201.3 Pa\) 和 \(1,202.8 Pa\)。与 S 型冷却通道相比，压降分别增加了 \(176\) 和 \(178 Pa\)，在可接受的范围内。

3.2 不同因素下的结果

为了得到冷却通道直径对电池散热的影响规律，冷却液流向为IIfd，冷却板初始厚度为 \(10 mm\)，冷却通道间距为 \(15 mm\)，其他边界条件一致。将直径作为单变量进行仿真分析。如图 4A所示、冷却通道直径对最高温度、温差和压降影响很大。最初，随着冷却通道直径的增大，最高温度、温差和压降迅速下降，但随着直径继续增大，下降速率变得明显平坦，表明直径尺寸的影响开始减弱。当直径为 7 毫米时，电池模组的最高温度与 6 毫米基本相同，温差略有增大。原因是直径的增加降低了冷却板表面的温度，电池模组底部的温度迅速下降，但顶部的温度变化不大，

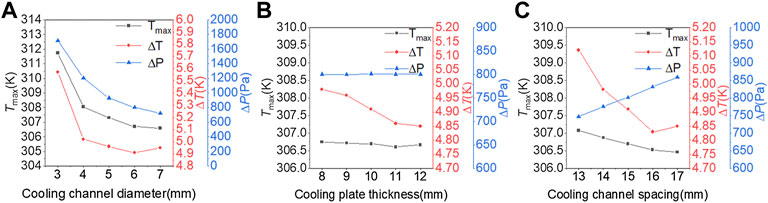
图 4 (A )冷却通道直径( B)冷却板厚度对\(T_ {max}\)、\(\Delta T\)和\(\Delta p\)的影响；(C)冷却通道间距

为了得到冷却板厚度对电池散热的影响规律，冷却液流向采用II fd，冷却管直径为 6 mm，间距为 15 mm，其余的边界条件是相同的。如图 4B所示随着冷却板厚度的增加，冷却板的散热面积增大，散热效率也提高，从而使电池模组的温差明显减小，但最高温度变化不大。当冷却板厚度为 12mm 时，电池模组的最高温度值变化不大，温差趋于平坦。另外，由于压降与冷却板的厚度变化没有直接关系，因此压降保持在相同水平。

如图 4C所示，当冷却通道直径为 6 mm、冷却板厚度为 11 mm 时，随着冷却通道间距增大，电池模组表面最高温度平缓下降，温差明显减小。分析表明，冷却板中冷却通道的体积分数增大，增大了冷却板与冷却液的换热面积，在一定程度上提高了冷却板的散热性能。但随着间距不断增大，当冷却通道间距为 17mm 时，电池的温差有一定程度的增大。另外，间距的增加也导致压降迅速上升。

3.3 冷却板结构优化

3.3.1 正交试验

分析表明，冷却通道直径、冷却板厚度和冷却通道间距三个因素对电池模组表面温度分布有重要影响。为了获得冷却板的最佳结构参数，采用正交试验方法对冷却板的结构进行优化。上述三个实验因素分别用字母 A、B、C 表示。根据单因素变量模拟的结果，每个实验因素有五个水平，并选择 \(L_{25} (5^3 )\)正交表。因子水平表如表 4所示。

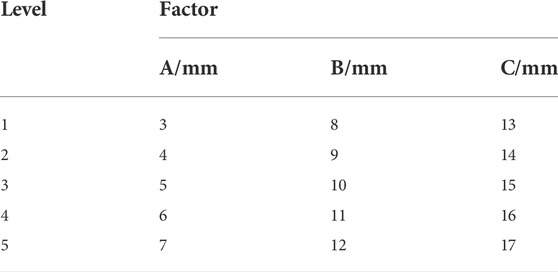
表 4 . 正交试验因子水平表

根据正交试验方案，分别建立各因素、各水平对应的仿真模型，并以\(T_ {max}\)、\(\Delta T\)和\(\Delta p\)作为评价指标。正交试验结果如表 5所示。整个正交试验结果的趋势如图 5所示。试验编号 21 的最高温度最小，试验编号 25 的温差最小，试验编号 22 的压降最小。

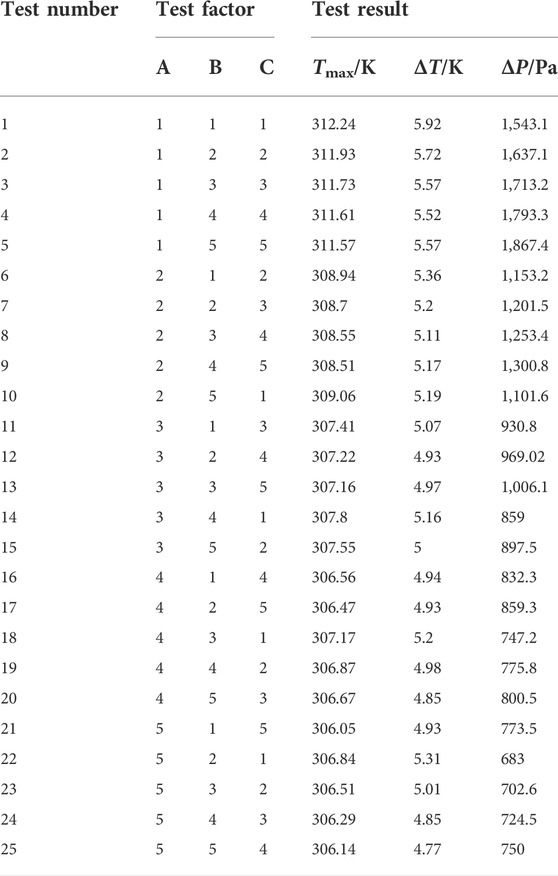
表 5. 正交试验结果

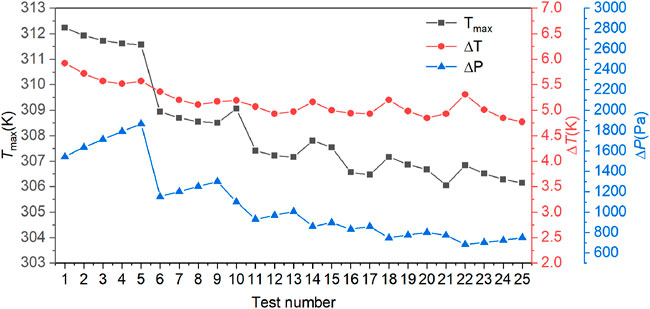
图 5 正交试验结果的趋势

3.3.2 极差分析

极差分析法（R 法）确定正交试验中各因素对 \(T_ {max}\)、\(\Delta T\)和\(\Delta p\)的影响程度。\(R\)值越大，说明该因素对试验指标的影响越大。本文用R j来表示第 j列因子的范围值。具体计算公式如下（Pan et al., 2019）：

\[ K_{jm}=\sum T_{\max jm} \]

\[ k_{jm}=\frac1nK_{jm} \]

\[ R_j=\max\left(k_{jm}\right)-min\left(k_{jm}\right) \]

其中\(K_{jm}\)为第\(j\)列因子的\(m\)级对应的测试指标总和；\(k_{jm}\)是 \(K_{jm}\)的平均值；\(n\) 是测试级别的数量；（\(j = A, B, C; m = 1,2,3,4,5\)）。

表 6显示极差分析的结果。三个实验因素对\(T_ {max}\)、\(\Delta T\)和\(\Delta p\)的影响程度顺序一致：\(A > C > B\)。冷却通道直径对各指标的影响最大，其次是冷却通道间距，最后是冷却板的厚度。对于最高温度指标，最优因子水平组合为 \(A_5 B_5 C_5\)，此时电池模块的最高温度最小。对于温差指标，最优因子水平组合为 \(A_5 B_5 C_4\)，此时电池模块的温差最小。对于压降指标，最优因子水平组合为 \(A_5 B_1 C_1\)，此时通道进出口压降最小。

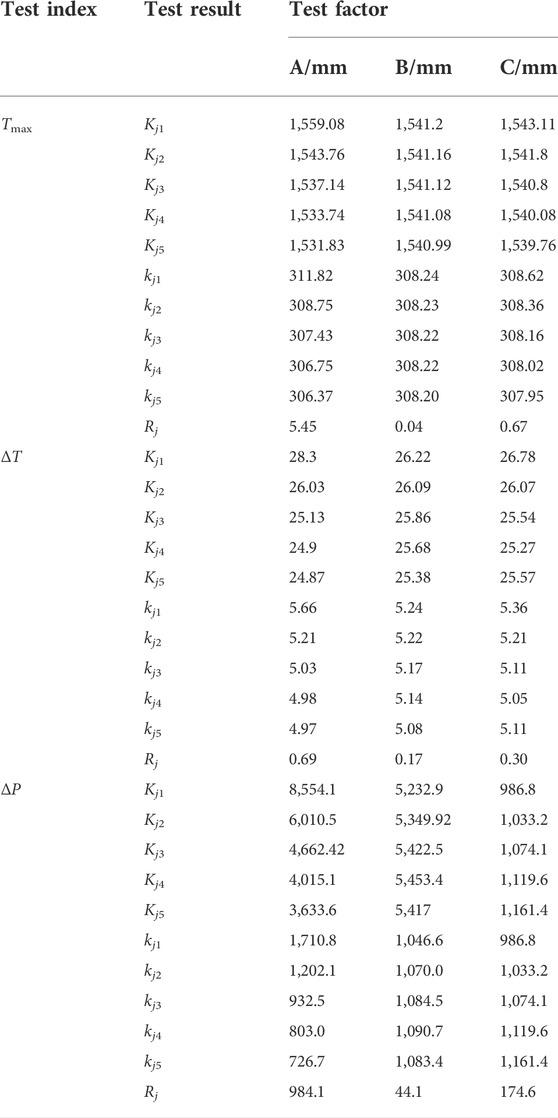
表 6 . 极差分析结果

在评估冷却板的冷却性能时，一般取决于电池模块的最高温度和温差。在最大程度满足电池散热要求的同时，还具有合理的压降。根据极差分析结果，因子 \(A\) 对最高温度、温差和压降指标影响最大。最佳因子水平为 \(5\)，因此冷却通道直径为 \(7 mm\)。因素 \(B\) 对三项指标的影响最小。电池模块最高温度和温差的最优因子水平均为 \(5\)。同时，在压降方面，最小压降的最优因子水平为 \(1\)，但根据图4B，可见冷却板的厚度对压降影响不大，因此冷却板的厚度为 \(12 mm\)。因素 C 对三项指标的影响程度位居第二。由表 5可知，4 级和 5 级的最大温度指标值相差不大，但温差指标相差较大，因此取温差指标值较小的 4 级，因此降温通道间距为 \(16 mm\)。最后综合考虑这三个指标，确定冷却板结构参数的最佳组合为 \(A_5 B_5 C_4\)。

4 结论

1）为了促进电池高效散热，设计了带有蜘蛛网状通道的冷却板。通过 CFD 建模发现这种新颖的结构能够有效降低电池模块的最大温度和温差。

2）S 型与 C 型仿真结果对比表明，蛛网状散热板散热效果较好，电池模组最高温度及温差较低，但通道压降稍小更高。其次，该结构中冷却剂的流动方向对电池模组的散热具有重要影响。与Ifd相比， IIfd流向冷却液整体温度分布更加均匀，冷却板表面温差更小，电池模组整体散热更好。

3）当冷却通道直径为 3∼7 mm、冷却板厚度为 8∼12 mm、通道间距为 13∼17 mm 时，冷却板的性能提高，电池模块的最大温度和温差提高随着直径、间距和厚度的增加而减小。正交试验结果发现，当冷却通道直径为 7 mm、冷却板厚度为 12 mm、间距为 16 mm 时，冷却板与电池之间的热交换效果最佳。综上所述，蛛网状通道冷却板为汽车动力锂离子电池热管理研究提供了一定的参考价值。

数据可用性声明

研究中提出的原始贡献包含在文章/补充材料中，进一步的询问可以直接联系通讯作者。

作者贡献

QZ 提供了研究的构思和设计并撰写了初稿。HW 指导了这项研究，支持了基金并修改了初稿。ZW 和 YF 为数据的统计和处理提供了思路。WC 为本研究提供了资源和硬件支持。

资金

该工作得到国家自然科学基金（51875419）、湖北省自然科学基金青年项目（2020CFB320）、湖北文理学院科研能力培养基金科技创新团队项目（2020kypytd007）的资助“新能源汽车与智能交通”湖北省优势特色学科群，电动汽车动力系统设计与测试湖北省重点实验室开放基金（ZDSYS202201、ZDSYS202208）。

利益冲突

作者声明，该研究是在不存在任何可能被视为潜在利益冲突的商业或财务关系的情况下进行的。

出版商备注

本文中表达的所有主张仅代表作者的主张，并不一定代表其附属组织或出版商、编辑和审稿人的主张。本文中可能评估的任何产品或其制造商可能提出的声明均未得到出版商的保证或认可。

参考

Al-Zareer, M., Dincer, I., and Rosen, M. (2019). A novel approach for performance improvement of liquid to vapor based battery cooling systems. Energy Convers. Manag. 187, 191–204. doi:10.1016/j.enconman.2019.02.063

Alipanah, M., and Li, X. (2016). Numerical studies of lithium-ion battery thermal management systems using phase change materials and metal foams. Int. J. Heat. Mass Transf. 102, 1159–1168. doi:10.1016/j.ijheatmasstransfer.2016.07.010

Behi, H., Karimi, D., Behi, M., Jaguemont, J., Ghanbarpour, M., Behnia, M., et al. (2020). Thermal management analysis using heat pipe in the high current discharging of lithium-ion battery in electric vehicles. J. Energy Storage 32, 101893. doi:10.1016/j.est.2020.101893

Bernardi, D., Pawlikowski, E., and Newman, J. (1985). A general energy balance for battery systems. J. Electrochem. Soc. 132 (1), 5–12. doi:10.1149/1.2113792

Choudhari, V., Dhoble, A., and Panchal, S. (2020). Numerical analysis of different fin structures in phase change material module for battery thermal management system and its optimization. Int. J. Heat. Mass Transf. 163, 120434. doi:10.1016/j.ijheatmasstransfer.2020.120434

Chung, Y., and Kim, M. (2019). Thermal analysis and pack level design of battery thermal management system with liquid cooling for electric vehicles. Energy Convers. Manag. 196, 105–116. doi:10.1016/j.enconman.2019.05.083

Deng, T., Ran, Y., Yin, Y., Chen, X., and Liu, P. (2019). Multi-objective optimization design of double-layered reverting cooling plate for lithium-ion batteries. Int. J. Heat. Mass Transf. 143, 118580. doi:10.1016/j.ijh-eatmasstransfer.2019.118580

Fan, Y., Wang, Z., Fu, T., and Wu, H. (2022). Numerical investigation on lithium-ion battery thermal management utilizing a novel tree-like channel liquid cooling plate exchanger. Int. J. Heat. Mass Transf. 183, 122143. doi:10.1016/j.ijheatmasstransfer.2021.122143

Huang, P., Verma, A., Robles, D., Wang, Q., Mukherjee, P., and Sun, J. (2018). Probing the cooling effectiveness of phase change materials on lithium-ion battery thermal response under overcharge condition. Appl. Therm. Eng. 132, 521–530. doi:10.1016/j.applthermaleng.2017.12.121

Huo, Y., Rao, Z., Liu, X., and Zhao, J. (2015). Investigation of power battery thermal management by using mini-channel cold plate. Energy Convers. Manag. 89, 387–395. doi:10.1016/j.enconman.2014.10.015

Imran, A., Mahmoud, N., and Jaffal, H. (2018). Numerical and experimental investigation of heat transfer in liquid cooling serpentine mini-channel heat sink with different new configuration models. Therm. Sci. Eng. Prog. 6, 128–139. doi:10.1016/j.tsep.2018.03.011

Kausthubharam, , Koorata, P., and Chandrasekaran, N. (2021). Numerical investigation of cooling performance of a novel air-cooled thermal management system for cylindrical Li-ion battery module. Appl. Therm. Eng. 193, 116961. doi:10.1016/j.applthermaleng.2021.116961

Li, Y., Du, Y., Xu, T., Wu, H., Zhou, X., Ling, Z., et al. (2018). Optimization of thermal management system for Li-ion batteries using phase change material. Appl. Therm. Eng. 131, 766–778. doi:10.1016/j.applthermaleng.2017.12.055

Lu, M., Zhang, X., Ji, J., Xu, X., and Zhang, Y. (2020). Research progress on power battery cooling technology for electric vehicles. J. Energy Storage 27, 101155. doi:10.1016/j.est.2019.101155

Pan, C., Tang, Q., He, Z., Wang, L., and Chen, L. (2019). Structure optimization of battery module with a parallel multi-channel liquid cooling plate based on orthogonal test. J. Electrochem. Energy Convers. Storage 17 (2). doi:10.1115/1.4045197

Patil, M., Seo, J., Panchal, S., and Lee, M. (2020). Numerical study on sensitivity analysis of factors influencing liquid cooling with double cold‐plate for lithium‐ion pouch cell. Int. J. Energy Res. 45 (2), 2533–2559. doi:10.1002/er.5946

Pradeep, R., and Venugopal, T. (2020). Experimental study of lithium-ion battery cooling using mixture of phase change materials. Int. J. Electr. Hybrid. Veh. 12 (2), 168. doi:10.1504/ijehv.2020.106354

Qian, Z., Li, Y., and Rao, Z. (2016). Thermal performance of lithium-ion battery thermal management system by using mini-channel cooling. Energy Convers. Manag. 126, 622–631. doi:10.1016/j.enconman.2016.08.063

Rao, Z., Qian, Z., Kuang, Y., and Li, Y. (2017). Thermal performance of liquid cooling based thermal management system for cylindrical lithium-ion battery module with variable contact surface. Appl. Therm. Eng. 123, 1514–1522. doi:10.1016/j.applthermaleng.2017.06.059

Rao, Z., Wang, Q., and Huang, C. (2016). Investigation of the thermal performance of phase change material/mini-channel coupled battery thermal management system. Appl. Energy 164, 659–669. doi:10.1016/j.apenergy.2015.12.021

Saw, L., Ye, Y., Tay, A., Chong, W., Kuan, S., and Yew, M. (2016). Computational fluid dynamic and thermal analysis of Lithium-ion battery pack with air cooling. Appl. Energy 177, 783–792. doi:10.1016/j.apenergy.2016.05.122

Sheng, L., Su, L., Zhang, H., Li, K., Fang, Y., Ye, W., et al. (2019). Numerical investigation on a lithium ion battery thermal management utilizing a serpentine-channel liquid cooling plate exchanger. Int. J. Heat. Mass Transf. 141, 658–668. doi:10.1016/j.ijheatmasstransfer.2019.07.033

Wilke, S., Schweitzer, B., Khateeb, S., and Al-Hallaj, S. (2017). Preventing thermal runaway propagation in lithium ion battery packs using a phase change composite material: An experimental study. J. Power Sources 340, 51–59. doi:10.1016/j.jpowsour.2016.11.018

Xie, J., Xie, Y., and Yuan, C. (2019). Numerical study of heat transfer enhancement using vortex generator for thermal management of lithium ion battery. Int. J. Heat. Mass Transf. 129, 1184–1193. doi:10.1016/j.ijheatmasstransfer.2018.10.018

Yan, Y., Yan, H., Yin, S., Zhang, L., and Li, L. (2019). Single/multi-objective optimizations on hydraulic and thermal management in micro-channel heat sink with bionic Y-shaped fractal network by genetic algorithm coupled with numerical simulation. Int. J. Heat. Mass Transf. 129, 468–479. doi:10.1016/j.ijheatmasstransfer.2018.09.120

Yang W, W., Zhou, F., Zhou, H., and Liu, Y. (2020). Thermal performance of axial air cooling system with bionic surface structure for cylindrical lithium-ion battery module. Int. J. Heat. Mass Transf. 161, 120307. doi:10.1016/j.ijheatmasstransfer.2020.120307

Yang Y, Y., Xu, X., Zhang, Y., Hu, H., and Li, C. (2020). Synergy analysis on the heat dissipation performance of a battery pack under air cooling. Ionics (Kiel) 26 (11), 5575–5584. doi:10.1007/s11581-020-03676-5

Yu, X., Lu, Z., Zhang, L., Wei, L., Cui, X., and Jin, L. (2019). Experimental study on transient thermal characteristics of stagger-arranged lithium-ion battery pack with air cooling strategy. Int. J. Heat. Mass Transf. 143, 118576. doi:10.1016/j.ijheatmasstransfer.2019.118576

Zhang, T., Gao, Q., Wang, G., Gu, Y., Wang, Y., Bao, W., et al. (2017). Investigation on the promotion of temperature uniformity for the designed battery pack with liquid flow in cooling process. Appl. Therm. Eng. 116, 655–662. doi:10.1016/j.applthermaleng.2017.01.069

Zhao, D., Li, S., and Zhao, H. (2016). Entropy-involved energy measure study of intrinsic thermoacoustic oscillations. Appl. Energy 177, 570–578. doi:10.1016/j.apenergy.2016.05.142